Оценка возможной доходности инвестиционного порфеля

Каждому инвестору рано или поздно приходит в голову идея оценки доходности собственного портфеля. Продолжаем цикл статей, раскрывающих различные методы финансового анализа.

В сегодняшей статье речь пойдет про некоторые основы математической статистики при инвестировании. Раскроем секреты того, как выразить в процентах вероятности ваших потерь и чего вообще следует ждать от собственного портфеля.

Доходности как случайная величина

Распределение вероятностей описывает вероятности всех возможных результатов для случайной величины, в нашем случае доходности).

Игральная кость (кубик) имеет самое простое распределение вероятностей. При броске одного традиционного кубика есть шесть возможных сценариев, вероятность наступления каждого из них равна 1/6, а сумма этих вероятностей — 1. Распределение вероятностей всех возможных значений индекса S&P500 в следующем году является более сложной версией той же идеи.

Если для какого-то события может быть предусмотрено конечное число возможных сценариев развития, то результаты этих сценариев называют дискретной случайной величиной. В таком случае для каждого возможного результата существует своя собственная вероятность наступления. Примером дискретной случайной величины является количество дней, в течение которых стоимость активов росла, поскольку существует конечное число возможных дней роста.

Для непрерывной случайной величины число возможных результатов бесконечно, даже если существуют нижняя и верхняя границы допустимых значений. Количество ежедневных осадков от нуля до 10 метров является примером непрерывной случайной величины, потому что оно может принимать бесконечное количество значений (при условии, что мы не будем округлять значение количества осадков до целого, как это обычно происходит)

В финансах доходности рассматриваются как непрерывные величины, поскольку число их возможных результатов очень велико. Например, увеличение или уменьшение цены акции, торгуемой на американской бирже, отражается в долларах и центах. Тем не менее, вероятность изменения ровно на 1,33$ или 1,34$ (или на любую другую конкретную величину) стремится к нулю. Поэтому принято говорить не о вероятности изменения цены до определённого значения, а о вероятности попадания цены в диапазон возможных её значений. Скажем, изменение цены до значения из диапазона от 1,00$ до 2,00$. Другими словами, вероятность равенства цены значению 1,33$, по сути, равна нулю, но вероятность её равенства значению из интервала от 1,33$ до 1,34$ уже больше нуля.

Стандартное распределение доходности

Функция плотности однозначно определяет для каждого значения доходности ее вероятность. Она хорошо визуализируется и из ее формы можно понять с какой частотой какая доходность будет появляться. На рисунке показан пример функции плотности для "стандартного нормального распределения", также называемого Гауссовым. Данное распределение и ее функция является центральной для всей математической статистики и применяется обычно в первую очередь.

Ось X - доход актива в долларах за день, ось Y - вероятностная плотность (читай, вероятность) для данного уровня доходности. Все графики ниже имеют аналогичную стрктуру.

Вероятность вычисляется как общая площадь под графиком слева от -1 по оси X. Как можно заметить, с вероятностью 15,87% доход составит меньше, чем -1 доллар. Примененное "стандартное нормальное распределение" характеризуется всего двумя параметрами: средним ожидаемым доходом и волатильностью. Наше распределение характеризуется всего двумя параметрами: средним ожидаемым доходом и волатильностью. На графике средняя доходность равна 0, а волатильность – 1. Для вычисления вероятностей можно воспользоваться довольно простыми «правилами сигм»:

• Доходность в пределах одной волатильности от среднего значения наступит с вероятностью 68,26%
• Доходность в пределах двух волатильностей от среднего значения наступит с вероятностью 95,44%
• Доходность в пределах трех волатильностей от среднего значения наступит с вероятностью 99,72%

На графике ниже изображены вероятности для каждого уровня доходности отдельно.

Распределения доходности с учетом черных лебедей

К сожалению, в жизни доходность подчиняется более сложным формам распределения вероятностей. История показала, что рынки практически каждое десятилетие отыгрывают сценарии, которые, следуя вышеописанной логике, должны были бы происходить всего раз в миллионы лет. Такие события с давних пор стали называть «чёрными лебедями». Поэтому статистиками были предложены альтернативные формы распределения доходностей, которые могут учитывать таких «лебедей».

У нас есть стандартное Гауссовское, которое применяется в идеальном мире, а есть еще логнормальное. На графике изображено логнормальное распределение(справа) по сравнению со стандартным (слева). Два наиболее примечательных свойства такого распределения заключаются в том, что оно не может показать доходность ниже -100% и при этом имеет незначительный шанс быть + 100500%. Благодаря этим свойствам логнормальное распределение хорошо отражает шанс банкротства компании или дефолта по облигации, но при этом предусматривает и возможность неограниченной прибыли.

Иные аналитические распределения имеют больше 2 параметров. Среди них могут встречаться такие свойства, как:

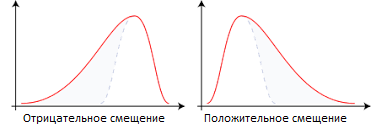
Коэффициент смещения (Skewness) является мерой несимметричности распределения доходности. В случае симметричного распределения коэффициент смещения равен нулю. При прочих равных условиях отрицательное значение асимметрии является предпочтительным. Именно смещение отвечает за психологический аспект торговли на бирже, когда в кризис все начинают массово продавать активы. При этом из-за этого смещения видно, что восстановление цен активов после каждого кризиса обычно происходит медленнее, чем предшествующее их падение.

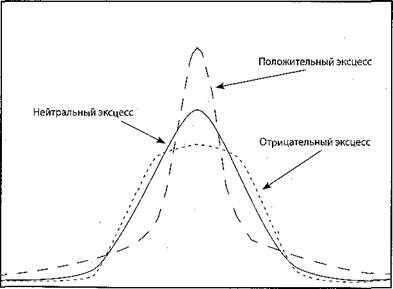
Эксцесс (Kurtosis) отражает относительную сгруппированность доходностей около среднего значения по сравнению с доходностями, чрезвычайно удалёнными от среднего значения.

Историческое моделирование

Историческое моделирование основано на фактических изменениях стоимости или факторов риска за некоторый предшествующий период.

Преимущество исторического моделирования заключается в использовании фактического распределения факторов доходности, благодаря чему отпадает необходимость поиска соответствующего распределения из области матстатистики. Основная проблема заключается в том, что прошлые доходности могут быть плохим показателем будущих доходностей. События, которые происходят редко, могут не отражаться в исторических результатах моделирования, если только эти события не произошли в течение выбранного для моделирования периода.

На сайте rusetfs.com имеются возможности для применения методов математической статистики на основе исторического моделирования. Рассмотрим етф на Америку FXUS, распределение его доходности и основные параметры. Все нижеописанные картинки взяты из соответствующего отчета сравнения FXUS с индексом S&P500.

1. CAGR — фактически это среднегодовая доходность. Чем больше это значение, тем лучше.
2. Volatility (ann.) — величина стандартного отклонения доходности от среднегодовой. Чем меньше это значение, тем меньше «сюрпризов» будет преподносить данный актив.
3. Skew — смещение доходности. Негативное значение Skew говорит о том, что доходность имеет склонность к бо́льшим положительным значениям. Положительное значение Skew предупреждает о том, что для доходности преобладает тенденция к резким падениям.
4. Kurtosis — мера собранности вокруг средней доходности. Чем выше значение Kurtosis, тем больше доходности произойдет вокруг средней. В итоге, учитывая все эти параметры, на графике распределение месячной доходности выглядит так:

Как видим, было уже 6 месяцев с доходностью ниже -10%, 3 месяца с доходностью -8% и 6 месяцев с доходностью -5%. Подобное поведение вызвано отрицательным значением Skew. Зато эксцесс положителен и основная масса месячных доходностей сосредоточена вокруг средней, что говорит об относительно одинаковых доходностях в спокойное время.

Выводы

Сегодня мы рассказали о распределении доходностей при инвестициях в фонды. Доходности бывают совершенно разные, но математики всё равно пытаются формализовать все эти процессы и найти Грааль. Множество квантовых аналитиков работает над более сложными формами распределения, создавая сверхприбыльные стратегии.

Примером успешного применения статистики является Renaissance Technologies LLC. Этот американский хедж-фонд специализируется на биржевой торговле с использованием количественных моделей. Он был основан в 1982 году Джеймсом Саймонсом, известным математиком, занимавшимся дешифровкой советских кодов во время холодной войны. Renaissance Technologies LLC славится лучшей историей доходности на Уолл-стрит, демонстрируя рентабельность более 66% годовых (до выплаты налогов, или 39% после уплаты налогов и сборов) в течение 30-летнего периода с 1988 по 2018 год. Однако «Ренессанс» открыт лишь для собственных сотрудников. Внешним инвесторам Renaissance предлагает два портфеля — Renaissance Institutional Equities Fund (RIEF) и Renaissance Institutional Diversified Alpha (RIDA).

Тем временем мы продолжаем нашу акцию анализа портфелей читателей. Первый, кто напишет на почту info@rusetfs.com письмо с темой "Матстат для моего портфеля!", получит уникальную возможность в индивидуальном порядке получить анализ своего портфеля. Вы получите анализ любого портфеля в виде привычного отчета сравнения портфелей, даже если в вашем портфеле имеются отличные от ETF активы. Это прекрасная возможность узнать и улучшить качество вашего управления собственными инвестициями.