Оценка рискованности инвестиционного порфеля

Каждому инвестору рано или поздно приходит в голову идея оценки рискованности собственного портфеля. В связи с поступающими вопросами по отчету в разделе "Симуляция портфеля" мы начинаем цикл статей, раскрывающих различные методы финансового анализа.

Коэффициент Шарпа (https://ru.wikipedia.org/wiki/Коэффициент_Шарпа, Sharpe ratio) — один из важных параметров анализа успешности инвестиционного портфеля. Он отражает то, насколько хорошо доходность актива компенсирует принимаемый инвестором риск. При сравнении двух активов с одинаковым ожидаемым доходом, вложение в актив с более высоким коэффициентом Шарпа будет менее рискованным. Отрицательный коэффициент Шарпа свидетельствует о том, что прибыльность инвестиционного портфеля ниже, чем прибыль, полученная от безрисковых инвестиций.

Важно помнить, что в финансовом мире под риском часто подразумевается любая волатильность, будь то приносящая убытки или доходы. Подобное заявление звучит нелогично, но без этого допущения дальнейшая математика не сработает.

Пример расчета коэффициента Шарпа

Формально выражаясь, коэффициент Шарпа отражает меру того, сколько инвестор получает сверх безрисковой ставки за принятие одной единицы риска портфеля.

Коэффициент Шарпа = (Доходность портфеля - Безрисковая ставка) / Стандартное отклонение доходности

В этой формуле годовая доходность по T-Bills или ОФЗ обычно используется для представления годовой безрисковой ставки.

Давайте объясним смысл формулы «на пальцах». Предположим, что доходность облигаций государственного займа (безрисковые инвестиции) составляет 6%.

Возьмем трейдера Васю:

• Доходность его инвестиций по 3 годам составила 15%, 20% и 3%. Средняя доходность (15+20+3)/3=12.67.
• Стандартное отклонение от безрисковой доходности составит √(15–12.67)²+(20–12.67)²+(3–12.67)²=12.3
• Коэффициент Шарпа вычисляется как (12.67–6)/12.3=0.54

А теперь трейдер Петя:

• Доходность его инвестиций по 3 годам составила 25%, 0% и 20%. Средняя доходность (25+0+20)/3=15
• Стандартное отклонение от безрисковой доходности составит √(25–15)²+(0–15)²+(20–15)²=18.7
• Коэффициент Шарпа вычисляется как (15–6)/18.7=0.48

Мы видим, что, хотя у трейдера Пети пиковая доходность и средняя доходность за период выше, чем у Васи, коэффициент Шарпа у Васи выше. Почему? Потому что у Пети слишком большие колебания доходности. То есть эту доходность он достигает за счет довольно большого риска. И оправдается ли этот привычный риск для Пети в будущем — вопрос.

Коэффициент Сортино

Коэффициент Сортино очень похож на коэффициент Шарпа. В отличие от Шарпа, в его знаменателе вместо стандартного отклонения доходности используется стандартное отклонение только убыточной доходности. Убыточная доходность - доходность ниже вашей средней доходности за весь период. Таким образом, Сортино учитывает только отрицательный риск, который приносит убытки инвестору. Данное свойство делает Сортино более подходящим для рядового инвестора, ведь в быту риском называют вероятность негативного события.

Коэффициент Сортино = (Доходность - Минимальная приемлемая доходность) / Стандартное отклонение только убыточной доходности

Калькулятор коэффициентов Шарпа и Сортино для вашего портфеля

На нашем сайте доступно множество рассчитанных показателей для вашего эмитируемого портфеля. Например, в отчете сравнения FXGD c IMOEX вы найдете полноценное сравнение динамики золота против российского индекса акций со множеством специфичных метрик. В данном отчете нас интересует два блока.

Поясняем все три графика:

1. Rolling volatility - стандартное отклонение котировок (волатильность) за последние 6 месяцев. Чем больше значение, тем более резкими и частыми были изменения динамики за последние 6 месяцев.
2. Rolling Sharpe - коэффициент Шарпа за последние 6 месяцев. Важно оценивать свой портфель не только в "моменте", но и относительно предыдущих периодов. Желательно, чтобы ваш портфель обладал Шарпом с меньшим количеством колебаний на графике. Как мы видим, у актива коэффициент шарпа очень чувствительный и меняется во времени от -2 до 2. Данное обстоятельство говорит нам о том, что Шарп у золота непостоянен и вознаграждение за единицу риска на разных временных промежутках разное.
3. Rolling Sortino - коэффициент Сортино за последние 6 месяцев. Обладает такими же свойствами, как и Шарп.

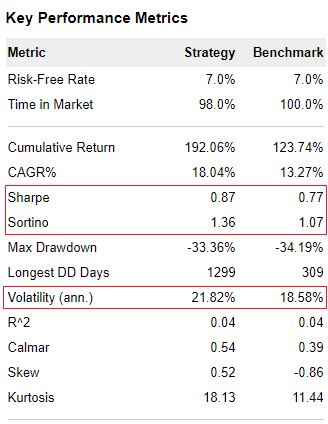
В правом блоке отчета имеется расчет трех показателей (Шарп, Сортино, Стандартное отклонение) за весь доступный период расчета. Он изменяется во времени гораздо медленнее, чем на графиках, так как период меньше. Значения в данном разделе обладают сглаживающим эффектом по отношению к кризисам и пузырям.

Такой же отчет доступен на вкладке каждого портфеля. Доступно сравнение с рынками мира, депозитами, инфляцией и курсом доллара.

Выбор менее рискованного актива

Как мы выяснили, Шарп и Сортино являются интересными показателями с точки зрения оценки как доходности, так и риска портфеля. Таким образом, включение в портфель актива с большим Шарпом будет приносить этому портфелю и больше надежности. Для отбора кандидатов можно воспользоваться следующими источниками.

В разделе Скринер имеется возможность отфильтровать все доступные ETF/БПИФ по риск-коэффициентам, а также во вкладке таблицы "Риск" посмотреть значения Шарпа и Сортино.

Дополнительно Шарп и Сортино указан в каждом ETF в разделе "Сравнение с Альтернативами". Например, на этой картинке сравниваются FXUS с прочими ETF с момента их создания.

Недостатки Шарпа

Применение риск-менеджмента при инвестировании в фонды в России еще не так развито, но зарубежные инвесторы уже взяли на вооружение данную методику и насобирали для нас граблей. Коэффициент Шарпа имеет ряд ограничений, которые желательно понимать инвестору:

• Коэффициент Шарпа нелинейно зависит от времени. При переходе от разных временных интервалов Шарп увеличивается пропорционально квадратному корню времени. Например, годовой коэффициент Шарпа будет в √12 больше, чем месячный коэффициент Шарпа.

• Чем меньше временной промежуток, взятый для измерения Шарпа, тем сильнее его чувствительность. Поэтому при сравнении двух фондов рекомендуется расчитывать Шарп за один и тот же промежуток времени.

• Шарп не является подходящей мерой оценки риска, когда инвестиции имеют асимметричное распределение прибыли с отрицательной или положительной асимметрией. К сожалению, доходность активов обычно представляется более сложным распределением. При применении Шарпа приходится пренебрегать данным обстоятельством.

• Неликвидные активы могут долго оставаться постоянными без изменения стоимости, занижая волатильность и смещая коэффициент Шарпа вверх.

• Не было обнаружено, что коэффициент Шарпа обладает прогнозирующей способностью для фондов в целом. На «победителя» по коэффициенту Шарпа за прошедший период нельзя рассчитывать, чтобы предсказать будущий успех.

Помимо недостатков, коэффициент Шарпа может быть сознательно изменен управляющим фонда. Коэффициент Шарпа может быть увеличен без реального эффекта, когда инвестиции действительно приносят более высокую доходность с поправкой на риск. В частности, Spurgin (2001) продемонстрировал следующие способы игры в оотношении Шарпа:

• Удлинение интервала измерения. Это приведет к снижению оценки волатильности; например, годовое стандартное отклонение дневной доходности обычно выше, чем еженедельное, которое, в свою очередь, выше, чем месячное.

• Игра с опционами. Эта стратегия может увеличить доходность, собирая опционную премию, не окупаясь в течение нескольких лет. Стратегии, предусматривающие принятие риска дефолта, риска ликвидности или других форм риска, обладают той же способностью смещать вверх коэффициент Шарпа. (Примерами являются коэффициенты Шарпа нейтральных на рынке хедж-фондов до и после кризиса ликвидности 1998 года.) Этот подход аналогичен обмену отрицательной асимметрии для увеличения коэффициента Шарпа путем улучшения среднего или стандартного отклонения инвестиций.

• Обмен экстремальных доходов (лучшие и худшие ежемесячные доходы каждый год) по свапу с третьим лицом. Подобный свап уменьшает стандартное отклонение, увеличивая Шарп. С практической точки зрения эта стратегия предусматривает обмен совокупной доходностью: каждый платит лучшую и худшую доходность по эталонному индексу каждый год, а контрагент платит фиксированный денежный поток и хеджирует риск на открытом рынке.

Вывод

Сегодня мы рассказали об относительных риск-метриках при инвестициях в фонды. Большая доходность - не единственный критерий для выбора ETF. Постоянство доходности является даже более важным фактором для долгосрочного инвестора, рассчитывающего на безбедную пенсию. Коэффициенты Шарпа и Сортино обьединяют доходность и постоянство в одну простую величину, отвечающую за сравнительное измерение риск-премий вашего портфеля.

Самое вкусное напоследок - специальная акция! Первый, кто напишет на почту info@rusetfs.com письмо с темой "Шарп для моего портфеля!", получит уникальную возможность в индивидуальном порядке получить анализ своего портфеля. Вы получите анализ любого портфеля в виде привычного отчета сравнения портфелей, даже если в вашем портфеле имеются отличные от ETF активы. Это прекрасная возможность узнать и улучшить качество вашего управления собственными инвестициями.